Question

Write a coordinate proof to prove that the segment that joins the vertex angle of an isosceles triangle to the midpoint of its base is perpendicular to the base .

Answer 1

Given: An Isosceles Triangle ABC with a vertex at B.

Midpoint M of the base AC.

To Prove: BM is perpendicular to AC.

Proof:

Let the coordinates of the points of the isosceles triangle be given as:

A = (-k, 0)

Vertex, B = (0,a)

C = (k, 0)

Midpoint, M = (0,0)

Slope of the base segment, AC:

`=(dy)/(dx) = (0 - 0)/(k - (-k)) = (0)/(2\cdot k)`

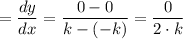
Slope of the base segment, AC=
`(0)/(2\cdot k)=0`

Slope of the segment that joins the vertex angle of an isosceles triangle to the midpoint of its base, BM.

`\text{Slope of BM =} (0 - a)/(0 - 0) = (-a)/(0)\\`

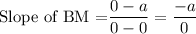
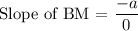`\text{Slope of BM = } (-a)/(0)` = Undefined

Two lines are perpendicular if the gradient of one is a negative reciprocal of the other.

Since
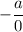`-(a)/(0)` is a negative reciprocal of 0 for arbitrary values of a, BM and AC are perpendicular.

This concludes the proof.