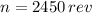Answer:
a)
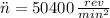 , b)
, b)
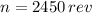
Step-by-step explanation:
a) The acceleration experimented by the grinding wheel is:
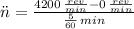
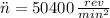
Now, the number of revolutions done by the grinding wheel in that period of time is:
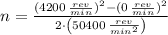

b) The acceleration experimented by the grinding wheel is:
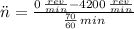
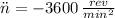
Now, the number of revolutions done by the grinding wheel in that period of time is: