Answer:
(a)

(b)
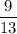
(c)
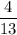
Explanation:
Number of cards in a Standard Deck=52
(a)
Number of Diamonds (D)=13
Number of Face Cards(F) = 12
Number of Diamonds that are face cards = 3
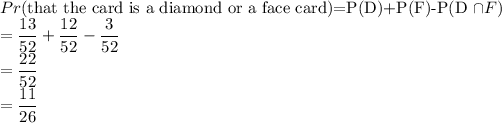
(b)The probability that the card is neither an ace nor a heart.
Number of Aces (A)=4
Number of Hearts(H) = 13
Number of Hearts that are Aces = 1

(c)The probability that the card is a face card or a 3
Number of 3 cards(T)=4
Number of Face Cards(F) = 12
