Answer:
56.4 m
Step-by-step explanation:
volume increases by factor of 6, i.e
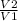 = 6
= 6
Initial temperature T1 at bottom of lake = 5.24°C = 278.24 K
Final temperature T2 at top of lake = 18.73°C = 291.73 K
NB to change temperature from °C to K we add 273
Final pressure P2 at the top of the lake = 0.973 atm
Initial pressure P1 at bottom of lake = ?
Using the equation of an ideal gas
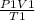 =
=
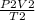
P1 =
 =
=
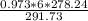
P1 = 5.57 atm
5.57 atm = 5.57 x 101325 = 564380.25 Pa
Density Ρ of lake = 1.02 g/
 = 1020 kg/
= 1020 kg/

acceleration due to gravity g = 9.81
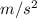
Pressure at lake bottom = pgd
where d is the depth of the lake
564380.25 = 1020 x 9.81 x d
d =
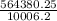 = 56.4 m
= 56.4 m