Answer:
The z-test statistic for a hypothesis test in which the null hypothesis states that the population proportion, p, equals 0.14 if the following sample information is present (n = 200; x = 31) is z = .6114.
Explanation:
The z-test statistic formula is:
We are given x = 31 and n = 200, so we can solve for
 : 31/200 = .155.
: 31/200 = .155.
The population proportion,
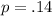 , is given in the problem.
, is given in the problem.
We can substitute the known values into the z test statistic formula:
The z-test statistic for this problem is z = .6114.