Question

What change(s) should Sylvia make to the equation to find the value of t in the above scenario?

Answer 1

Option (D).

Explanation:

Initial population of the deer
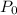`P_(0)` = 4800

Decrease in the population of the deer after every 8 years =
`(1)/(2)* (\text{Initial population})`

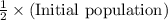
Decrease in population is an exponential process, so the expression representing population will be,

`P_(t)=P_(0)(1-r)^x`

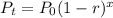
Where
`P_(t)` is the population after 'x' slots of 8 years.

r = fraction of decrease in the population

x =
`\frac{\text{Number of years}}{8}`

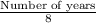
By substituting the values of r and x in the expression,

`P_(t)=P_(0)(1-(1)/(2))^{(t)/(8)}`

`P_(t)=4800((1)/(2))^{(t)/(8)}`

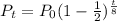
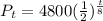
Therefore, Sylvia should do few corrections in her expression.

(8) should be replaced by (
`(1)/(2)`) and
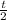`(t)/(2)` should be replaced by
`(t)/(8)`.

Option D. will be the answer.