Question

Alex and Bryan are giving an exam. The probability Alex gets an A is 0.9, the probability Bryan gets an A is 0.8 and the probability Alex gets an A and Bryan doesn't get an A is 0.1. What is the probability that either Alex or Bryan get an A.

Answer 1

The probability that either Alex or Bryan get an A is 0.9

Explanation:

Before we proceed to answer, we shall be making some important notation;

Let A = event of Alex getting an A

Let B = event of Bryan getting an A

From the question, P(A) = 0.9, P(B) = 0.8 and P(A ∩
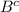`B^(c)` ) = 0.1

We are to calculate the probability that either Alex or Bryan get an A which can be represented as P(A ∪ B)

We can use the addition theorem here;

P(A ∪ B) = P(A) + P(B) - P(A ∩ B) .......................(i)

Also,

P(A) = P(A ∩
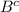`B^(c)` ) + P(A ∩ B) .........................(ii)

We can insert ii into i and we have;

P(A ∪ B) = P(A ∩
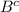`B^(c)` ) + P(A ∩ B) + P(B) - P(A ∩ B) = P(A ∩
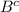`B^(c)` ) + P(B) = 0.1 + 0.8 = 0.9