Question

A solid square rod is cantilevered at one end. The rod is 0.6 m long and supports a completely reversing transverse load at the other end of 62 kN. The material is AISI 1080 hot-rolled steel. If the rod must support this load for 104 cycles with a design factor of 1.5, what dimension should the square cross section have

Answer 1

The dimension of the square cross section is = 30mm * 30mm

Step-by-step explanation:

Before proceeding with the calculations convert MPa to Kpsi

Sut ( ultimate strength ) = 770 MPa * 0.145 Kpsi/MPa = 111.65 Kpsi

the fatigue strength factor of Sut at 10^3 cycles for Se = Se' = 0.5 Sut

at 10^6 cycles" for 111.65 Kpsi = f ( fatigue strength factor) = 0.83

To calculate the endurance limit use Se' = 0.5 Sut since Sut < 1400 MPa

Se'( endurance limit ) = 0.5 * 770 = 385 Mpa

The surface condition modification factor

Ka = 57.7 ( Sut )^-0.718

Ka = 57.7 ( 770 ) ^-0.718

Ka = 0.488

Assuming the size modification factor (Kb) = 0.85 and also assuming all modifiers are equal to one

The endurance limit at the critical location of a machine part can be expressed as :

Se = Ka*Kb*Se'

Se = 0.488 * 0.85 * 385 = 160 MPa

Next:

Calculating the constants to find the number of cycles

α =
`((fSut)^2)/(Se)`

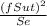
α =
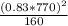`((0.83*770)^2)/(160)` = 2553 MPa

b =
`-(1)/(3) log((fSut)/(Se) )`

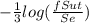
b =
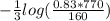`-(1)/(3) log ((0.83*770)/(160) )` = -0.2005

Next :

calculating the fatigue strength using the relation

Sf = αN^b

N = number of cycles

Sf = 2553 ( 10^4) ^ -0.2005

Sf = 403 MPa

Calculate the maximum moment of the beam

M = 2000 * 0.6 = 1200 N-m

calculating the maximum stress in the beam

∝ = ∝max =
`(Mc)/(I)`

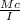
Where c = b/2 and I = b(b^3) / 12

hence ∝max =
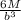`(6M)/(b^3)` = 6(1200) / b^3 = 7200/ b^3 Pa

note: b is in (meters)

The expression for the factor of safety is written as

n =
`(Sf)/(\alpha max )`

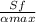
Sf = 403, n = 1.5 and ∝max = 7200 / b^3

= 1.5 =
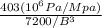`(403(10^6 Pa/Mpa))/(7200 / B^3)` making b subject of the formula in other to get the value of b

b = 0.0299 m * 10^3 mm/m

b = 29.9 mm therefore b ≈ 30 mm

since the size factor assumed is near the calculated size factor using this relation : de = 0.808 ( hb)^1/2

the dimension = 30 mm by 30 mm