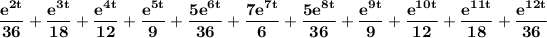Question

A fair die is rolled twice, with outcomes X for the first roll and Y for the second roll. Find the moment generating function MX`Y ptq of X ` Y . Note that your answer should be a function of t and can contain unsimplified finite sums.

Answer 1

`\mathbf{(e^(2t))/(36) + (e^(3t))/(18) + (e^(4t))/(12) +(e^(5t))/(9) + (5e^(6t))/(36) + (7e^(7t))/(6) + (5e^(8t))/(36) + (e^(9t))/(9) + (e^(10t))/(12) + (e^(11t))/(18) + (e^(12t))/(36) }`

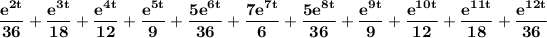
Explanation:

The objective is to find the moment generating function of
`M_(X+Y)(t) \ of \ X+Y`.

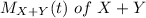We are being informed that the fair die is rolled twice;

So; X to be the value for the first roll

Y to be the value of the second roll

The outcomes of X are: X = {1,2,3,4,5,6}

Where ;

`P (X=x) = (1)/(6)`

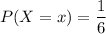
The outcomes of Y are: y = {1,2,3,4,5,6}

Where ;

`P (Y=y) = (1)/(6)`

The outcome of Z = X+Y

`= \left[\begin{array}{cccccc}(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\ (2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\ (3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6) \\ (4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6) \\ (5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6) \\ (6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6) \end{array}\right]`

= [2,3,4,5,6,7,8,9,10,11,12]

Here;

`P (Z=z) = (1)/(36)`

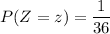
∴ the moment generating function
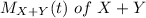`M_(X+Y)(t) \ of \ X+Y`is as follows:

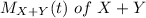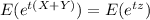
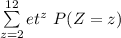
`M_(X+Y)(t) \ of \ X+Y` =
`E(e^(t(X+Y))) = E(e^(tz))`

⇒
`\sum \limits^(12)_ {z=2 } et ^z \ P(Z=z)`

=
`\mathbf{(e^(2t))/(36) + (e^(3t))/(18) + (e^(4t))/(12) +(e^(5t))/(9) + (5e^(6t))/(36) + (7e^(7t))/(6) + (5e^(8t))/(36) + (e^(9t))/(9) + (e^(10t))/(12) + (e^(11t))/(18) + (e^(12t))/(36) }`