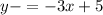Answer:
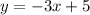
Explanation:
to find the gradient/slope between these points:
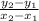
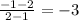
the gradient is -3
we need to write the equation in the form y=mx+c. Choose any of the two coordinates in the question. I'll choose (1,2).
y is 2, x is 1 and m is the gradient which is -3
working out c:
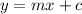
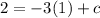
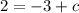
add 3 on both sides
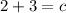
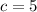
final equation: