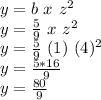Question

Find the constant of variation for the relation and use it to write and solve the equation.

if y varies directly as x and as the square of z, and y=25/9 when x=5 and z=1, find y when x=1 and z=4

Answer 1

When x = 1 and z = 4,
`y=(80)/(9)`

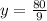
Explanation:

The variation described in the problem can be written using a constant of proportionality "b" as:

`y=b\,\,x\,\,z^2`

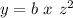
The other piece of information is that when x = 5 and z = 1, then y gives 25/9. So we use this info to find the constant "b":

`y=b\,\,x\,\,z^2\\(25)/(9) =b\,\,(5)\,\,(1)^2\\(25)/(9) =b\,\,(5)\\b=(5)/(9)`

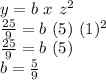
Knowing this constant, we can find the value of y when x=1 and z=4 as:

`y=b\,\,x\,\,z^2\\y=(5)/(9) \,\,x\,\,z^2\\y=(5)/(9) \,\,(1)\,\,(4)^2\\y=(5*16)/(9)\\y=(80)/(9)`