Question

Use the method of cylindrical shells to find the volume of the solid generated by rotating the region bounded by the curves y=cos(πx/2), y=0, x=0, and x=1 about the y-axis

Answer 1

1,45 cubic units

Explanation:

The method of cylindrical shells demands that the volume of the solid is given by:

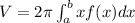`V=2\pi\int_a^b xf(x)dx` (1)

In this case you have that f(x) is:

`f(x)=cos((\pi)/(2)x)`

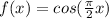
a = 0

b = 1

First, you solve the integral, by parts:

`\int xf(x)dx=\int xcos((\pi)/(2)x)dx=x((2)/(\pi))sin((\pi)/(2)x)-\int ((2)/(\pi))sin((\pi)/(2)x)dx\\\\=((2)/(\pi))xsin((\pi)/(2)x)+((2)/(\pi))^2cos((\pi)/(2)x)+C`

Next, you calculate the volume of the solid, by replacing the solution to the integral in the equation (1):

`V=2\pi[((2)/(\pi))xsin((\pi)/(2)x)+((2)/(\pi))^2cos((\pi)/(2)x)]_0^1\\\\V=2\pi[((2)/(\pi))-((2)/(\pi))^2]=1,45u^3`

hence, the volume of the solid generated is 1,45 cubic units