Question

A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of 85.0 0 to the initial direction of the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final velocity (magnitude and direction) of the bowling ball.

Answer 1

9.05 m/s , -14.72° (respect to x axis)

Step-by-step explanation:

To find the final velocity of the bowling ball you take into account the conservation of the momentum for both x and y component of the total momentum. Then, you have:

`p_(xi)=p_(xf)\\\\p_(yi)=p_(yf)\\\\`

`m_1v_(1xi)+m_2v_(2xi)=m_1v_1cos\theta+m_2v_(2)cos\phi\\\\0=m_1v_1sin\theta-m_2v_2sin\phi`

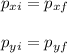
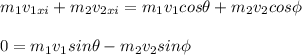
m1: mass of the bowling ball = 5.50 kg

m2: mass of the bowling pin = 0.850 kg

v1xi: initial velocity of the bowling ball = 9.0 m/s

v2xi: initial velocity of bowling pin = 0m/s

v1: final velocity of bowling ball = ?

v2: final velocity of bowling pin = 15.0 m/s

θ: angle of the scattered bowling pin = ?

Φ: angle of the scattered bowling ball = 85.0°

Where you have used that before the bowling ball hits the pin, the y component of the total momentum is zero.

First you solve for v1cosθ in the equation for the x component of the momentum:

`v_1cos\theta=(m_1v_(1xi)-m_2v_2cos\phi)/(m_1)\\\\v_1cos\theta=((5.50kg)(9.0m/s)-(0.850kg)(15.0m/s)cos85.0\°)/(5.50kg)\\\\v_1cos\theta=8.79m/s`

and also you solve for v1sinθ in the equation for the y component of the momentum:

`v_1sin\theta=((0.850kg)(15.0m/s)sin(85.0\°))/(5.50kg)\\\\v_1sin\theta=2.3m/s`

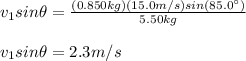
Next, you divide v1cosθ and v1sinθ:

`(v_1sin\theta)/(v_1cos\theta)=tan\theta=(2.3)/(8.79)=0.26\\\\\theta=tan^(-1)(0.26)=14.72`

the direction of the bawling ball is -14.72° respect to the x axis

The final velocity of the bawling ball is:

`v_1=(2.3m/s)/(sin\theta)=(2.3)/(sin(14.72\°))=9.05(m)/(s)`

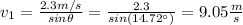
hence, the final velocity of the bawling ball is 9.05 m/s