Question

asked May 22, 2021 146k views

1 Answer

Anthony Martin · Answer 1 · 2021-05-26T13:42:31+0000

Answer:

A.
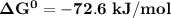$\mathbf{\Delta G^0 = -72.6 \ kJ/mol}$ ; as such the reaction is said to be spontaneous since the value of
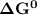$\mathbf{\Delta G^0 }$ is negative.

B.
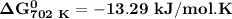$\mathbf{\Delta G^0_(702 \ K) = -13.29 \ kJ/mol.K}}$ and the reaction is spontaneous

Step-by-step explanation:

The equation for this chemical reaction is :

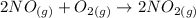
$2NO_((g)) +O_(2(g)) \to 2NO_(2(g))$

Using the following relation to calculate
$\Delta G^0$ ;

$\Delta G^0 = [2(\Delta G^0_{NO_(2(g))}] - [1(\Delta G^0_{O_(2(g))})+ 2(\Delta G^0_{NO_(g)})]$

At 298 K; the standard Gibbs Free Energy for the formation are as follows:

$\Delta G^0_{NO_(2(g))} = 51.2 \ kJ/mol$

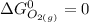
$\Delta G^0_{O_(2(g))} = 0$

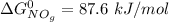
$\Delta G^0_{NO_(g)}= 87.6 \ kJ/mol$

Replacing them into the above equation;

$\Delta G^0 = [2(51.2 \ kJ/mol}] - [1(0)+ 2(87.6 \ kJ/mol})]$

$\Delta G^0 = [102.4 \ kJ/mol}] - [175.2 \ kJ/mol})]$

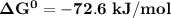
$\mathbf{\Delta G^0 = -72.6 \ kJ/mol}$

Thus;
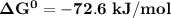$\mathbf{\Delta G^0 = -72.6 \ kJ/mol}$ ; as such the reaction is said to be spontaneous since the value of
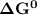$\mathbf{\Delta G^0 }$ is negative.

B.

Using the same above chemical equation;

The relation used for calculating
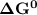$\mathbf{\Delta G^0}$ of the reaction when the temperature is 702 K is:

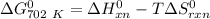
$\Delta G^0_(702 \ K) = \Delta H^0_(xn) - T \Delta S^0_(rxn)$

where;

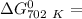$\Delta G^0_(702 \ K) =$ Gibbs free energy of the reaction at 702 K

$\Delta H^0_(xn)$ = standard enthalpy of the reaction = -116.2 kJ/mol

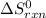$\Delta S^0_(rxn)$ = standard entropy of the reaction = -146.6 J/mol/K

Temperature T = 702 K

$\Delta G^0_(702 \ K) = -1162. \ kJ/mol - 702 \ K ( -146.6 \ J/mol. K ((1 \ kJ )/(1000 \ J))$

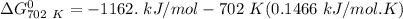
$\Delta G^0_(702 \ K) = -1162. \ kJ/mol - 702 \ K ( 0.1466 \ kJ/mol.K})$

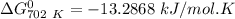
$\Delta G^0_(702 \ K) = -13.2868 \ kJ/mol.K}$

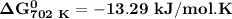
$\mathbf{\Delta G^0_(702 \ K) = -13.29 \ kJ/mol.K}}$

Thus
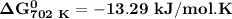$\mathbf{\Delta G^0_(702 \ K) = -13.29 \ kJ/mol.K}}$ and the reaction is spontaneous

Please log in or register to add a comment.