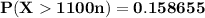Answer:
the approximate probability that the insurance company will have claims exceeding the premiums collected is
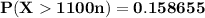
Explanation:
The probability of the density function of the total claim amount for the health insurance policy is given as :
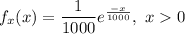
Thus, the expected total claim amount
 = 1000
= 1000
The variance of the total claim amount
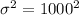
However; the premium for the policy is set at the expected total claim amount plus 100. i.e (1000+100) = 1100
To determine the approximate probability that the insurance company will have claims exceeding the premiums collected if 100 policies are sold; we have :
P(X > 1100 n )
where n = numbers of premium sold

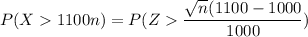
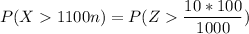
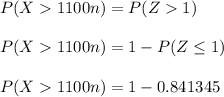
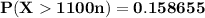
Therefore: the approximate probability that the insurance company will have claims exceeding the premiums collected is