Question

Which of the following describes the growth rate of the exponential function in the graph below?

For each x increase of 1, they increases by a common difference of 3.
For each x increase of 1, the y increases by a common factor of 3.
For each x increase of 1, the y increases by 4 more than the previous increase.
For each x increase of 1, they increases by doubling and then adding 1.

Answer 1

For each x increase of 1, the y increases by a common factor of 3.

Step-by-step explanation: hope it helps ^w^

Answer 2

For each x increase of 1, the y increases by a common factor of 3. (second answer listed)

Explanation:

Notice that you have not provided the graph that the problem involves, but from the description of what the y behavior is when x increases by one, one can deduct if an exponential pattern applies.

Out of the four examples given, only one of them represents an exponential growth. Such type of growth has to include a common multiplicative factor (the base of the exponent), since the function has to be of the form:

`f(x)=a\,\,b^x`

to be called exponential.

So every time that x increases by one unit, the following happens:

`f(x+1)=a\,\,b^((x+1))\\f(x+1)= a\,\,b^x\,\,b`

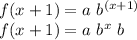
So notice that the original function ends up being just multiplied by the common factor "b".

The other options don't describe such behavior.