Answer:
a) 0.3085
b) 2574
c) 0.0125
Explanation:
mean (μ) = 2600 kcal/day and a standard deviation (σ) = 50 kcal/day
a) The z score is given by:

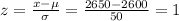
From the normal distribution table, P(x > 2650) = P(z > 1) = 1 - P(z < 1) = 1 - 0.8413 = 0.1587
b) A probability of 30% corresponds with a z score of -0.52
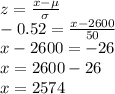
c) For a sampling distribution of sample mean, the standard deviation is
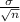
The z score is given by:
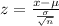
n = 20

From the normal distribution table, P(x > 2625) = P(z > 2.24) = 1 - P(z < 2.24) = 1 - 0.9875 = 0.0125