Question

The total energy need during pregnancy is normally distributed, with a mean of 2600 kcal/day and a standard deviation of 50 kcal/day. Include your Normal curve for all parts! a) [4 pts] If one pregnancy is randomly selected, find the probability that the total energy need is more than 2650 kcal/day. b) [4 pts] The middle 30% of total energy need during pregnancy are between what values? c) [4 pts] What is the probability that a random sample of 20 pregnant women has a mean energy need of more than 2625 kcal/day?

Answer 1

a) 0.3085

b) 2574

c) 0.0125

Explanation:

mean (μ) = 2600 kcal/day and a standard deviation (σ) = 50 kcal/day

a) The z score is given by:

`z=(x-\mu)/(\sigma)`

`z=(x-\mu)/(\sigma)=(2650-2600)/(50)=1`

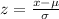
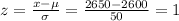
From the normal distribution table, P(x > 2650) = P(z > 1) = 1 - P(z < 1) = 1 - 0.8413 = 0.1587

b) A probability of 30% corresponds with a z score of -0.52

`z=(x-\mu)/(\sigma)\\-0.52=(x-2600)/(50) \\x-2600=-26\\x=2600-26\\x=2574`

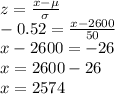
c) For a sampling distribution of sample mean, the standard deviation is
`(\sigma)/(√(n) )`

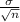
The z score is given by:

`z=(x-\mu)/((\sigma)/(√(n) ))`

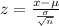
n = 20

`z=(x-\mu)/((\sigma)/(√(n) ))=(2625-2600)/((50)/(√(20) ))=2.24`

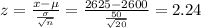
From the normal distribution table, P(x > 2625) = P(z > 2.24) = 1 - P(z < 2.24) = 1 - 0.9875 = 0.0125