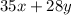Question

Retro Recyclers processes used plastics into milk containers and soda containers. The recycling plant can process up to 2000 tons of plastic a week. At least 900 tons must be processed for milk containers and at least 600 tons must be processed for soda containers. Retro earns $35 per tons for milk containers and $28 per ton for soda containers. Retro wants to figure out how many tons of plastic should be allocated for milk containers and how many tons for soda containers in order to maximize its weekly profit.

Define the variables, write the constraints, and write the objective function for this situation.

Answer 1

Objective function:

Maximize profit P =
`35x+28y`

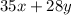
subject to following constraints:

`x\geq 900\\y\geq 600`

`x+y\leq 2000\\x\geq 0\,,\,y\geq 0`

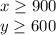
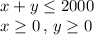
Explanation:

Given: The recycling plant can process up to 2000 tons of plastic a week. At least 900 tons must be processed for milk containers and at least 600 tons must be processed for soda containers.

Also, Retro earns $35 per tons for milk containers and $28 per ton for soda containers.

To find: objective function for the given situation

Solution:

Let x tons be used to make a milk container and y tones be used to make a soda container.

As at least 900 tons must be processed for milk containers and at least 600 tons must be processed for soda containers,

`x\geq 900\\y\geq 600`

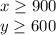
Also, as the recycling plant can process up to 2000 tons of plastic a week,

`x+y\leq 2000`

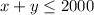
Also,
`x\geq 0\,,\,y\geq 0`

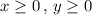
Objective function:

Maximize profit P =
`35x+28y`