Question

A package of 10 batteries is checked to determine if there are any dead batteries. Four batteries are checked. If one or more are dead, the package is not sold. What is the probability that the package will not be sold if there are actually three dead batteries in the package

Answer 1

There is a probability of 76% of not selling the package if there are actually three dead batteries in the package.

Explanation:

With a 10-units package of batteries with 3 dead batteries, the sampling can be modeled as a binomial random variable with:

• n=4 (the amount of batteries picked for the sample).
• p=3/10=0.3 (the proportion of dead batteries).
• k≥1 (the amount of dead batteries in the sample needed to not sell the package).

The probability of having k dead batteries in the sample is:

`P(x=k) = \dbinom{n}{k} p^(k)q^(n-k)`

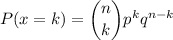
Then, the probability of having one or more dead batteries in the sample (k≥1) is:

`P(x\geq1)=1-P(x=0)\\\\\\P(x=0) = \dbinom{4}{0} p^(0)q^(4)=1*1*0.7^4=0.2401\\\\\\P(x\geq1)=1-0.2401=0.7599\approx0.76`