Question

Under normal operating conditions, the electric motor exerts a torque of 2.8 kN-m.on shaft AB. Knowing that each shaft is solid, determine the maximum shearing stress in a) shaft AB b) shaft BC c) shaft CD (25 points) Given that the torque at B

Answer 1

Step-by-step explanation:

The image attached to the question is shown in the first diagram below.

From the diagram given ; we can deduce a free body diagram which will aid us in solving the question.

IF we take a look at the second diagram attached below ; we will have a clear understanding of what the free body diagram of the system looks like :

From the diagram; we can determine the length of BC by using pyhtagoras theorem;

SO;

`L_(BC)^2 = L_(AB)^2 + L_(AC)^2`

`L_(BC)^2 = (3.5+2.5)^2+ 4^2`

`L_(BC)= √((6)^2+ 4^2)`

`L_(BC)= √(36+ 16)`

`L_(BC)= √(52)`

`L_(BC)= 7.2111 \ m`

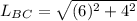
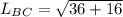
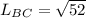
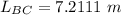
The cross -sectional of the cable is calculated by the formula :

`A = (\pi)/(4)d^2`

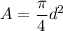
where d = 4mm

`A = (\pi)/(4)(4 \ mm * (1 \ m)/(1000 \ mm))^2`

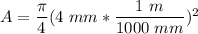
A = 1.26 × 10⁻⁵ m²

However, looking at the maximum deflection in length
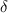`\delta` ; we can calculate for the force
`F_{BC` by using the formula:

`\delta = (F_(BC)L_(BC))/(AE)`

`F_(BC) = ( AE \ \delta)/(L_(BC))`

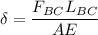
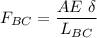
where ;

E = modulus elasticity

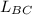`L_(BC)` = length of the cable

Replacing 1.26 × 10⁻⁵ m² for A; 200 × 10⁹ Pa for E ; 7.2111 m for
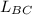`L_(BC)` and 0.006 m for
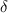`\delta` ; we have:

`F_(BC) = (1.26*10^(-5)*200*10^9*0.006)/(7.2111)`

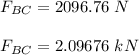`F_(BC) = 2096.76 \ N \\ \\ F_(BC) = 2.09676 \ kN` ---- (1)

Similarly; we can determine the force
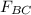`F_(BC)` using the allowable maximum stress; we have the following relation,

`\sigma = (F_(BC))/(A)`

`{F_(BC)}= {A}*\sigma`

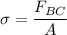
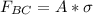
where;

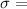`\sigma =` maximum allowable stress

Replacing 190 × 10⁶ Pa for
`\sigma` ; we have :

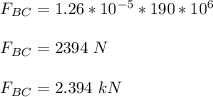`{F_(BC)}= 1.26*10^(-5) * 190*10^(6) \\ \\ {F_(BC)}=2394 \ N \\ \\ {F_(BC)}= 2.394 \ kN` ------ (2)

Comparing (1) and (2)

The magnitude of the force
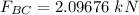`F_(BC) = 2.09676 \ kN` since the elongation of the cable should not exceed 6mm

Finally applying the moment equilibrium condition about point A

`\sum M_A = 0`

`3.5 P - (6) ( (4)/(7.2111)F_(BC)) = 0`

`3.5 P - 3.328 F_(BC) = 0`

`3.5 P = 3.328 F_(BC)`

`3.5 P = 3.328 *2.09676 \ kN`

`P =( 3.328 *2.09676 \ kN)/(3.5 )`

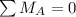
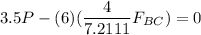
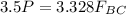
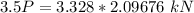
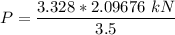
P = 1.9937 kN

Hence; the maximum load P that can be applied is 1.9937 kN