Question

Graph the image of the figure after a dilation with a scale factor of 3 centered at (2, −7). Use the Polygon tool to graph the quadrilateral by connecting all its vertices.

Answer 1

Here's what I get.

Explanation:

Assume the figure is like Image 1 below.

We must dilate each point by a scale factor of 3 centred at (2, −7).

1. Determine the transformation rules

Each point moves to three times its original distance from the centre.

Let P = a point on the figure and

let O = the centre of dilation

and L = the distance from the point to the centre. Then

L = P - O

Three times that distance is

3L = 3P - 3O

We want to find the point P' that is 3L from O, so we add this distance to the coordinates of O.

P' = 3L + O = 3P - 3O + O = 3P + 2O

If P is at (x,y) and O is at (h,k), the transformation rule is

(x,y) ⟶ (3x - 2h, 3y - 2k)

2. Make a table of the new coordinates

`\begin{array}{cclc}\textbf{Point} & \mathbf{(x,y)} &\textbf{Image Coordinates } \mathbf{(3x - 2h, 3y - 2k)}&\mathbf{(x',y')} \\A & (-2,-7) & (-6,-21) -2(2,-7) = (-6 - 4, -21 + 14) & (-10,-7) \\B & (0,-4) & (0,-12) -2(2,-7) = (0 - 4, -12 + 14)& (-4,2) \\C & (3,-3) & (9,-9) -2(2,-7) = (9 - 4, -9 + 14) & (5,5) \\D & (4,-5) & (12,-15) -2(2,-7) = (12 - 4, -15 +14) & (8,-1) \\\end{array}`

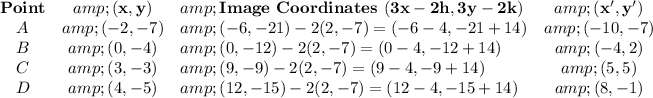
3. Graph the new shape

You should get a graph like Fig. 2.

The rays from Point O pass through corresponding points in the two shapes, so this is a dilation about O.

Point B is two units left of O and three units up.

Also, B' is six units left and nine units up, so the scale factor is three.