Question

X and Y are both standard normal random variables (mean = 0, standard deviation = 1), statistically independent of each other. Using the DATA IN THE ATTACHED FILE, estimate the probability that X and Y are both positive and that their sum is less or equal to 1. This probability is

Answer 1

The probability that X and Y are both positive and that their sum is less or equal to 1 0.64.

Explanation:

It is provided that the random variables X and Y follows a standard normal distribution.

That is,
`X,Y\sim N(0, 1)`

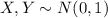
It is also provided that the variables X and Y are statistically independent of each other.

Compute the probability that X and Y are both positive and that their sum is less or equal to 1 as follows:

The mean and standard deviation of X + Y are:

`E(X+Y)=E(X)+E(Y)=0+0=0\\\\SD(X+Y)=√(V(X)+V(Y)+2Cov(X,Y))=√(1+1+0)=√(2)`

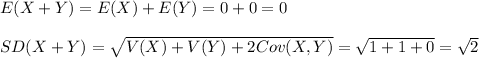
The probability is:

`P(X+Y\leq 1)=P(X+Y<1-0.50)\ [\text{Apply continuity correction}]\\`

`=P(X+Y<0.50)\\\\=P(((X+Y)-E(X+Y))/(SD(X+Y))<(0.50-0)/(√(2)))\\\\=P(Z<0.354)\\\\=0.63683\\\\\approx 0.64`

*Use the z-table.

Thus, the probability that X and Y are both positive and that their sum is less or equal to 1 0.64.