Question

A 330-km-long high-voltage transmission line 2.00 cm in diameter carries a steady current of 1,110 A. If the conductor is copper with a free charge density of 8.50 1028 electrons per cubic meter, how many years does it take one electron to travel the full length of the cable? (Use 3.156 107 for the number of seconds in a year.)

Answer 1

t = 402 years

Step-by-step explanation:

To find the number of year that electrons take in crossing the complete transmission line, you first calculate the drift speed of the electrons. Then, you use the following formula for the current in a wire:

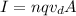`I=nqv_dA` (1)

n: number of mobile charge carrier per volume = 8.50*10^28 e/m^3

q: charge of the electron = 1.6*10^-19 C

vd: drift velocity of electron in the metal = ?

A: cross sectional area of the wire = π r^2 = π (0.02m/2)^2 = 3.1415*10^-4 m^2

I: current in the wire = 1110 A

You solve the equation (1) for vd:

`v_d=(I)/(nqA)=(110A)/((8.50*10^(28)m^(-3))(1.6*10^(-19)C)(3.1415*10^(-4)m^2))\\\\v_d=2.59*10^(-4)m/s`

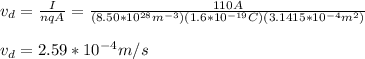
Next, you calculate the time by using the information about the length of the line transmission:

`x=v_dt\\\\x=330km=330000m\\\\t=(x)/(v_d)=(330000m)/(2.59*10^(-4)m/s)=1,270,184,865s\\\\1,270,184,865s*(1\ year)/(3,156,107)=402.45\ years`

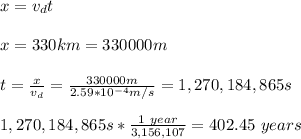
hence, the electrons will take aproximately 402 years in crossing the line of transmission