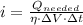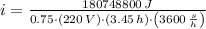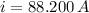Question

(a) What is the cost of heating a hot tub containing 1440 kg of water from 10.0°C to 40.0°C, assuming 75.0% efficiency to take heat loss to surroundings into account? The cost of electricity is 9.00¢/(kW · h) and the specific heat for water is 4184 J/(kg · °C). $ 67 Incorrect: Your answer is incorrect. How much heat is needed to raise the temperature of m kg of a substance? How many joules are in 1 kWh? (b) What current was used by the 220 V AC electric heater, if this took 3.45 h? 88.2 Correct: Your answer is correct. A

Answer 1

a)
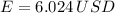`E = 6.024\,USD`, For m kilograms, it is 4184m J., 3600000 joules, b)
`i = 88.200\,A`

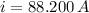
Step-by-step explanation:

a) The amount of heat needed to warm water is given by the following expression:

`Q_(needed) = m_(w)\cdot c_(w)\cdot (T_(f)-T_(i))`

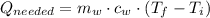
Where:

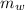`m_(w)` - Mass of water, measured in kilograms.

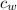`c_(w)` - Specific heat of water, measured in
`(J)/(kg\cdot ^(\circ)C)`.

`T_(f)`,
`T_(i)` - Initial and final temperatures, measured in
`^(\circ)C`.

Then,

`Q_(needed) = (1440\,kg)\cdot \left(4184\,(J)/(kg\cdot ^(\circ)C) \right)\cdot (40^(\circ)C - 10^(\circ)C)`

`Q_(needed) = 180748800\,J`

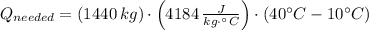
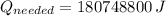
The energy needed in kilowatt-hours is:

`Q_(needed) = 180748800\,J* \left((1)/(3600000)\,(kWh)/(J) \right)`

`Q_(needed) = 50.208\,kWh`

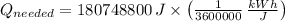
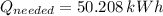
The electric energy required to heat up the water is:

`E = (50.208\,kWh)/(0.75)`

`E = 66.944\,kWh`

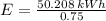
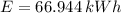
Lastly, the cost of heating a hot tub is: (USD - US dollars)

`E = (66.944\,kWh)\cdot \left(0.09\,(USD)/(kWh) \right)`

`E = 6.024\,USD`

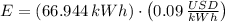
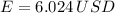
The heat needed to raise the temperature a degree of a kilogram of water is 4184 J. For m kilograms, it is 4184m J. Besides, a kilowatt-hour is equal to 3600000 joules.

b) The current required for the electric heater is:

`i = (Q_(needed))/(\eta \cdot \Delta V \cdot \Delta t)`

`i = (180748800\,J)/(0.75\cdot (220\,V)\cdot (3.45\,h)\cdot \left(3600\,(s)/(h) \right))`

`i = 88.200\,A`