Question

At LaGuardia Airport for a certain nightly flight, the probability that it will rain is

0.18 and the probability that the flight will be delayed is 0.14. The probability that it

will not rain and the flight will leave on time is 0.74. What is the probability that the

flight would leave on time when it is not raining? Round your answer to the thousand

Answer 1

0.902 = 90.2% probability that the flight would leave on time when it is not raining

Explanation:

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

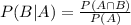
In which

P(B|A) is the probability of event B happening, given that A happened.

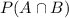`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Not raining

Event B: Flight leaving on time.

The probability that it will rain is 0.18.

This means that there is a 1 - 0.18 = 0.82 probability of not raining. So
`P(A) = 0.82`

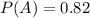
The probability that it will not rain and the flight will leave on time is 0.74.

This means that
`P(A \cap B) = 0.74`

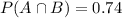
What is the probability that the flight would leave on time when it is not raining?

`P(B|A) = (0.74)/(0.82) = 0.902`

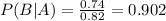
0.902 = 90.2% probability that the flight would leave on time when it is not raining