Question

An automobile manufacturer is concerned about a fault in the braking mechanism of a particular model. The fault can, on rare occasions, cause a catastrophe at high speed. The distribution of the number of cars per year that will experience the catastrophe is a random variable with variance = 5.

a) What is the probability that at most 3 cars per year will experience a catastrophe?
b) What is the probability that more than 1 car per year will experience a catastrophe?

Answer 1

(a) Probability that at most 3 cars per year will experience a catastrophe is 0.2650.

(b) Probability that more than 1 car per year will experience a catastrophe is 0.9596.

Explanation:

We are given that the distribution of the number of cars per year that will experience the catastrophe is a Poisson random variable with variance = 5.

Let X = the number of cars per year that will experience the catastrophe

SO, X ~ Poisson(
`\lambda = 5`)

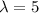The probability distribution for Poisson random variable is given by;

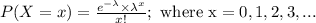
`P(X=x) = (e^(-\lambda) * \lambda^(x) )/(x!) ; \text{ where} \text{ x} = 0,1,2,3,...`

where,
`\lambda` = Poisson parameter = 5 {because variance of Poisson distribution is
`\lambda` only}

(a) Probability that at most 3 cars per year will experience a catastrophe is given by = P(X
`\leq` 3)

P(X
`\leq` 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

=
`(e^(-5) * 5^(0) )/(0!) +(e^(-5) * 5^(1) )/(1!) +(e^(-5) * 5^(2) )/(2!) +(e^(-5) * 5^(3) )/(3!)`

=
`e^(-5) +(e^(-5) * 5) +(e^(-5) * 25 )/(2) +(e^(-5) * 125)/(6)`

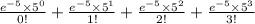
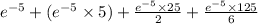
= 0.2650

(b) Probability that more than 1 car per year will experience a catastrophe is given by = P(X > 1)

P(X > 1) = 1 - P(X
`\leq` 1)

= 1 - P(X = 0) - P(X = 1)

=
`1-(e^(-5) * 5^(0) )/(0!) -(e^(-5) * 5^(1) )/(1!)`

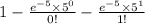
= 1 - 0.00674 - 0.03369

= 0.9596