Question

An English teacher needs to pick 10 books to put on her reading list for the next school year, and she needs to plan the order in which they should be read. She has narrowed down her choices to 4 novels, 6 plays, 8 poetry books, and 4 nonfiction books. Step 1 of 2 : If she wants to include no more than 3 poetry books, how many different reading schedules are possible? Express your answer in scientific notation rounding to the hundredths place.

Answer 1

the number of possible reading schedules is 1.064301638 × 10¹²

Explanation:

Given that :

The English teacher needs to pick 10 books to put on her reading list for the next school year.

If the English teacher picks at most 3 poetry books i.e no more than 3 poetry books from 8 books. and other books are picked from (6+4+4 ) = 14 books

Thus; the number of ways to pick the books are :

`\left[\begin{array}{c}8\\0\\ \end{array}\right] \ \left[\begin{array}{c}14\\10\\ \end{array}\right]+ \left[\begin{array}{c}8\\1\\ \end{array}\right] \left[\begin{array}{c}14\\9\\ \end{array}\right] + \left[\begin{array}{c}8\\2\\ \end{array}\right] \left[\begin{array}{c}14\\8\\ \end{array}\right] + \left[\begin{array}{c}8\\3\\ \end{array}\right] \left[\begin{array}{c}14\\7 \\ \end{array}\right]`

`= [ (8!)/(0!(8-0)!)* (14!)/(10!(14-10!)) ] + [ (8!)/(1!(8-1)!)* (14!)/(9!(14-9)!)]+ [ (8!)/(2!(8-2)!)* (14!)/(8!(14-8)!)] + [ (8!)/(3!(8-3)!)* (14!)/(7!(14-7)!)]`

`= [ 1*1001]+[8*2002]+[28*3003]+[56*3432]`

`\mathbf{= 293293}`

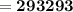
However, to determine how many reading schedules that are possible we use the relation:

Number of ways to pick a book ×
`^(10)P_(10)`

`= 293293* (10!)/((10-10)!)`

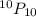
= 293293 × 10!

= 1.064301638 × 10¹²

Thus , the number of possible reading schedules is 1.064301638 × 10¹²