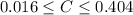Question

Small sample: During an economic downturn, companies were sampled and asked whether they were planning to increase their workforce. Only of the companies were planning to increase their workforce. Use the small-sample method to construct a confidence interval for the proportion of companies that are planning to increase their workforce. Round the answers to at least three decimal places. A confidence interval for the proportion of companies that are planning to increase their workforce is .

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The confidence level interval is
`0.016 \le C \le 0.404`

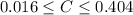
Explanation:

The sample size is
`n = 20`

The number planning to increase workforce is
`x = 3`

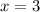
The confidence level is
`c = 98`%

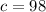The value of proportion for a plus 4 method is

`p = (x+2)/(n+4)`

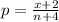
substituting values

`p = (3+2)/(20+4)`

`p =0.21`

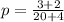
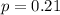
The z-critical value at confidence level of 98% is

`z_(c)=z_(0.98) = 2.33`

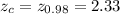
This values is obtained from the standard normal table

The confidence level interval can be mathematically represented as

`C =p \ \pm z_(c) * \sqrt{(p(1-p))/(n+4) }`

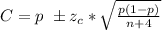
substituting values

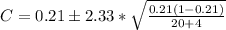
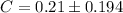
`C = 0.21 \pm 2.33 * \sqrt{(0.21(1- 0.21))/(20 +4) }`

`C = 0.21 \pm 0.194`

=>
`0.016 \le C \le 0.404`