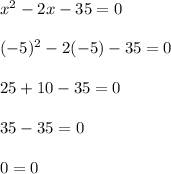Question

Use factoring to solve
x^2-2x-35=0

Answer 1

I'm sorry I don't have an answer but for all future math work you should download photomath on your phone it's rly good

Answer 2

The solution set of the quadratic equation is

x = {7, -5}

Explanation:

Given the quadratic equation

`$ x^2 - 2x -35 = 0 $`

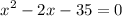
We need to factor this equation

So you need two numbers such that

a + b = -2

and

a×b = -35

How about -7 and 5?

-7 + 5 = -2

-2 = -2

and

-7×5 = -35

-35 = -35

(x - 7)(x + 5) = 0

(x - 7) = 0

x = 7

and

(x + 5) = 0

x = -5

Therefore, the solution set of the quadratic equation is

x = {7, -5}

Verification:

Plug 7 into the quadratic equation

`x^2 - 2x -35 = 0 \\\\(7)^2 - 2(7) -35 = 0 \\\\49 - 14 - 35 = 0 \\\\49 - 49 = 0\\\\0 = 0`

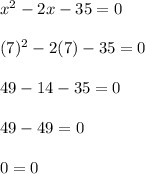
Plug -5 into the quadratic equation

`x^2 - 2x -35 = 0 \\\\(-5)^2 - 2(-5) -35 = 0 \\\\25 + 10 - 35 = 0 \\\\35 - 35 = 0\\\\0 = 0`