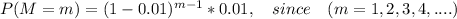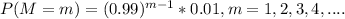Question

Problem 3.3.9 • (a) Starting on day 1, you buy one lottery ticket each day. Each ticket is a winner with probability 0.1. Find the PMF of K, the number of tickets you buy up to and including your fifth winning ticket. (b) L is the number of flips of a fair coin up to and including the 33rd occurrence of tails. What is the PMF of L? (c) Starting on day 1, you buy one lottery ticket each day. Each ticket is a winner with probability 0.01. Let M equal the number of tickets you buy up to and including your first winning ticket. What is the PMF of M?

Answer 1

a) The probability mass function of K =
`P(K=k) = \binom{k-1}{4}0.1^(4)*0.9^(k-5) ; k =5,6,...`

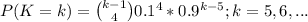
b)

c)

Explanation:

a) Let p be the probability of winning each ticket be = 0.1

Then q which is the probability of failing each ticket = 1 - p = 1 - 0.1 = 0.9

Assume X represents the number of failure preceding the 5th success in x + 5 trials.

The last trial must be success whose probability is p = 0.1 and in the remaining (x + r- 1) ( x+ 4 ) trials we must have have (4) successes whose probability is given by:

`\binom{x+r-1}{r-1}*p^(r-1)*q^(x) = \binom{x+4}{4}0.1^(4)*0.9^(x) ; x =0, 1, .........`

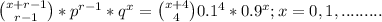
Then, the probability distribution of random variable X is

`P(X=x) = \binom{x+4}{4}0.1^(4)*0.9^(x) ; x =0, 1, .........`

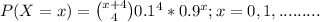
where;

X represents the negative binomial random variable.

K= X + 5 = number of ticket buy up to and including fifth winning ticket.

Since K =X+5 this signifies that X = K-5

as X takes value 0, 1 ,2,...

K takes value 5, 6 ,...

Therefore:

The probability mass function of K =
`P(K=k) = \binom{k-1}{4}0.1^(4)*0.9^(k-5) ; k =5,6,...`

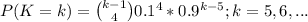
b)

Let p represent the probability of getting a tail on a flip of the coin

Thus p = 0.5 since it is a fair coin

where L = number of flips of the coin including 33rd occurrence of tails

Thus; the negative binomial distribution of L can be illustrated as:

`P(X=x) = \binom{x-1}{r-1}(1-p)^(x-r)p^r`

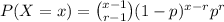
where

X= L

r = 33 &

p = 0.5

Since we are looking at the 33rd success; L is likely to be : L = 33,34,35...

Thus; the PMF of L =
`P(L=l) = \binom{l-1}{33-1}(1-0.5)^(l)(0.5)^(33) \\ \\ \\ \mathbf{P(L=l) = \binom{l-1}{33-1}(0.5)^(l) }`

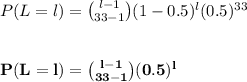
c)

Given that:

Let M be the random variable which represents the number of tickets need to be bought to get the first success,

also success probability is 0.01.

Therefore, M ~ Geo(0.01).

Thus, the PMF of M is given by:

`P(M = m) = (1-0.01)^(m-1) * 0.01 , \ \ \ since \ \ \ (m = 1,2,3,4,....)`

`P(M=m) = (0.99)^(m-1) * 0.01 , m = 1,2,3,4,....`