Question

4. The average annual income of 100 randomly chosen residents of Santa Cruz is $30,755 with a standard deviation of $20,450. a) What is the standard deviation of the annual income? b) Test the hypothesis that the average annual income is $32,000 against the alternative that it is less than $32,000 at the 10% level. c) Test the hypothesis that the average annual income is equal to $33,000 against the alternative that it is not at the 5% level. d) What is the 95% confidence interval of the average annual income?

Answer 1

a) The standard deviation of the annual income σₓ = 2045

b)

The calculated value Z = 0.608 < 1.645 at 10 % level of significance

Null hypothesis is accepted

The average annual income is greater than $32,000

c)

The calculated value Z = 1.0977 < 1.96 at 5 % level of significance

Null hypothesis is accepted

The average annual income is equal to $33,000

d)

95% of confidence intervals of the Average annual income

(26 ,746.8 ,34, 763.2)

Explanation:

Given size of the sample 'n' =100

mean of the sample x⁻ = $30,755

The Standard deviation = $20,450

a)

The standard deviation of the annual income σₓ =
`(S.D)/(√(n) )`

=
`(20,450)/(√(100) )= 2045`

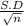
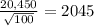
b)

Given mean of the Population μ = $32,000

Given size of the sample 'n' =100

mean of the sample x⁻ = $30,755

The Standard deviation ( σ)= $20,450

Null Hypothesis:- H₀: μ > $32,000

Alternative Hypothesis:H₁: μ < $32,000

Level of significance α = 0.10

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (30755-32000 )/((20450)/(√(100) ) )`

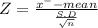
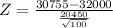
Z= |-0.608| = 0.608

The calculated value Z = 0.608 < 1.645 at 10 % level of significance

Null hypothesis is accepted

The average annual income is greater than $32,000

c)

Given mean of the Population μ = $33,000

Given size of the sample 'n' =100

mean of the sample x⁻ = $30,755

The Standard deviation ( σ)= $20,450

Null Hypothesis:- H₀: μ = $33,000

Alternative Hypothesis:H₁: μ ≠ $33,000

Level of significance α = 0.05

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (30755-33000 )/((20450)/(√(100) ) )`

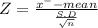
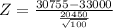
Z = -1.0977

|Z|= |-1.0977| = 1.0977

The 95% of z -value = 1.96

The calculated value Z = 1.0977 < 1.96 at 5 % level of significance

Null hypothesis is accepted

The average annual income is equal to $33,000

d)

95% of confidence intervals is determined by

`(x^(-) - 1.96 (S.D)/(√(n) ) , x^(-) + 1.96 (S.D)/(√(n) ))`

`(30755 - 1.96 (20450)/(√(100) ) , 30755 +1.96 (20450)/(√(100) ))`

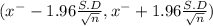
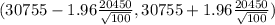
( 30 755 - 4008.2 , 30 755 +4008.2)

95% of confidence intervals of the Average annual income

(26 ,746.8 ,34, 763.2)