Question

A glucose solution is administered intravenously into the bloodstream at a constant rate r. As the gulcose is added, it is converted into other substances and removed from the bloodstream at a rate that is proportional to the concentration at the time. Thus a model for the concentration C=C(t) of the glucose solution in the bloodstream is

dC/dt=r-kC
Where r an dk are positive constants.
1. Suppose that the concentration at time t=0 is C0. Determine the concentration at any time t by solving the differential equation.
2. Assuming that C0

Answer 1

`C(t) =( r)/(k) - \left ((r-kC_(0))/(k) \right )e^( -kt)`

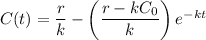
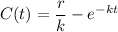`C(t) =( r)/(k)- e^( -kt)` ,thus, the function is said to be an increasing function.

Explanation:

Given that:

`(dC)/(dt)= r-kC`

`(dC)/(r-kC)= dt`

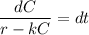
Taking integration on both sides ;

`\int\limits(dC)/(r-kC)= \int\limits \ dt`

`- (1)/(k)In (r-kC)= t +D`

`In(r-kC) = -kt - kD \\ \\ r- kC = e^(-kt - kD) \\ \\ r- kC = e^(-kt) e^( - kD) \\ \\r- kC = Ae^(-kt) \\ \\ kC = r - Ae^(-kt) \\ \\ C = (r)/(k) - (A)/(k)e ^(-kt) \\ \\`

`C(t) =( r)/(k) - (A)/(k)e^( -kt)`

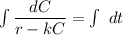
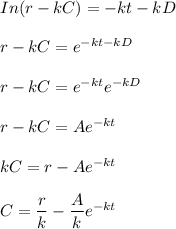
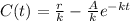
here;

A is an integration constant

In order to determine A, we have
`C(0) = C0`

`C(0) =( r)/(k) - (A)/(k)e^(0)`

`C_0 =(r)/(k)- (A)/(k)`

`C_(0) =( r-A)/(k)`

`kC_(0) =r-A`

`A =r-kC_(0)`

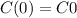
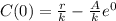
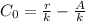
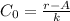
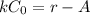
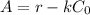
Thus:

`C(t) =( r)/(k) - \left ((r-kC_(0))/(k) \right )e^( -kt)`

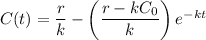
2. Assuming that C0 < r/k, find lim t→[infinity] C(t) and interpret your answer

`C_(0) < \lim_(t \to \infty )C(t) \\ \\C_0 < (r)/(k) \\ \\kC_0 <r`

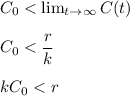
The equation for C(t) can be rewritten as :

`C(t) =( r)/(k) - \left ((r-kC_(0))/(k) \right )e^( -kt)C(t) =( r)/(k) - \left (+ve \right )e^( -kt) \\ \\C(t) =( r)/(k)- e^( -kt)`

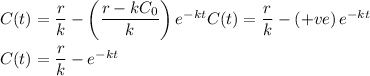
Thus; the function is said to be an increasing function.