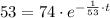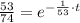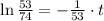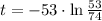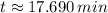Question

The differential equation below models the temperature of a 91°C cup of coffee in a 17°C room, where it is known that the coffee cools at a rate of 1°C per minute when its temperature is 70°C. Solve the differential equation to find an expression for the temperature of the coffee at time t. dy dt = − 1 53 (y − 17)\

Answer 1

`t \approx 17.690\,min`

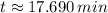
Explanation:

This differential equation is a first order linear differential equation with separable variables, whose solution is found as follows:

`(dy)/(dt) = - (1)/(53) \cdot (y - 17)`

`(dy)/(y-17) = -(1)/(53) \, dt`

`\int\limits^(y)_{y_(o)} {(dy)/(y-17) } = -(1)/(53) \int\limits^(t)_(0)\, dx`

`\ln \left |(y-17)/(y_(o)-17) \right | = -(1)/(53) \cdot t`

`(y-17)/(y_(o)-17) = e^{-(1)/(53)\cdot t }`

`y = 17 + (y_(o) - 17) \cdot e^{-(1)/(53)\cdot t }`

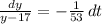
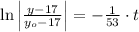
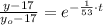
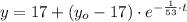
The solution of the differential equation is:

`y = 17 + 74\cdot e^{-(1)/(53)\cdot t }`

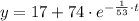
Where:

`y` - Temperature, measured in °C.

`t` - Time, measured in minutes.

The time when the cup of coffee has the temperature of 70 °C is:

`70 = 17 + 74 \cdot e^{-(1)/(53)\cdot t }`

`53 = 74 \cdot e^{-(1)/(53)\cdot t }`

`(53)/(74) = e^{-(1)/(53)\cdot t }`

`\ln (53)/(74) = -(1)/(53)\cdot t`

`t = - 53\cdot \ln (53)/(74)`

`t \approx 17.690\,min`