Answer:
the total work W = 29.05 kJ
the change in total internal energy is
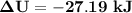
the total heat transferred in [kJ] is Q = 1.860 kJ
Step-by-step explanation:
Given that
mass of carbon dioxide in the closed system = 1 kg
Temperature
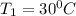 = (273+30 ) K = 303 K
= (273+30 ) K = 303 K
Pressure
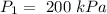
Pressure
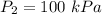
polytropic expansion n = 1.27
Note that we are also given the following data set:
R = 188.9 J/kg.K
c_v = 655 J/kg.K
So; for a polytropic process ;
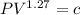
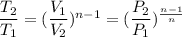
![T_2 = T_1 [(P_2)/(P_1)]^{(n-1)/(n)](https://img.qammunity.org/2021/formulas/business/college/jdnsg1drd5av20714gma7umrlc9207uwoh.png)
![T_2 = 303 [(100)/(200)]^{(1.27-1)/(1.27)](https://img.qammunity.org/2021/formulas/business/college/hyf0457bke029vo7wn0roi0b5p3el0vbwn.png)

Since the system does not follow the first order of thermodynamics; To calculate the total work by using the expression:
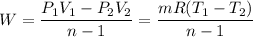
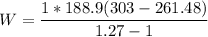
W = 29048.62222 J
W = 29.05 kJ
Thus, the total work W = 29.05 kJ
The change in internal energy can be expressed by the formula:
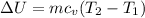
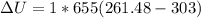
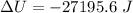
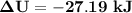
Hence; the change in total internal energy is
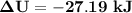
Finally; to determine the total heat transferred in [kJ]; we go by the expression for the first order of thermodynamics which say:
Total Heat Q = ΔU + W
Q = (-27.19 + 29.05)kJ
Q = 1.860 kJ
Hence; the total heat transferred in [kJ] is Q = 1.860 kJ