Answer:
a) The CDF of X/Y is calculated as:
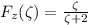 for
for
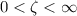
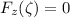 for
for

Note: Z = X/Y
b) Probability that A finishes before B = 1/3
Explanation:
For clarity and easiness of expression, this solution is handwritten and attached as a file. Check the complete solution in the attached file.