Complete Question
The complete question is shown on the first uploaded image
Answer:
The mass is

Step-by-step explanation:
From the question we are told that
The mass of the stars are
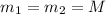
The orbital speed of each star is
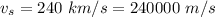
The orbital period is
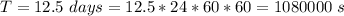
The centripetal force acting on these stars is mathematically represented as
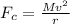
The gravitational force acting on these stars is mathematically represented as
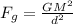
So
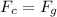
=>

=>
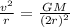
=>

=>
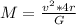
The distance traveled by each sun in one cycle is mathematically represented as
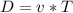
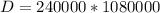

Now this can also be represented as
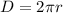
Therefore
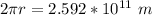
=>
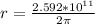
=>
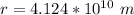
So
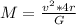
=>
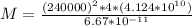
=>
