Question

The guy wires AB and AC are attached to the top of the transmission tower. The tension in cable AB is 8.7 kN. Determine the required tension T in cable AC such that the net effect of the two cables is a downward force at point A. Determine the magnitude R of this downward force.

Answer 1

`T_A_C = 6.296 kN`

`R = 10.06 kN`

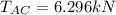
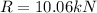
Step-by-step explanation:

Given:

`T_A_B = 8.7 kN`

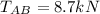
Required:

Find the tension TAC and magnitude R of this downward force.

First calculate
`\alpha, \beta, \gamma`

`\alpha = tan^-^1 =(40)/(50) = 38. 36`

`\beta = tan^-^1 =(50)/(30) = 59.04`

`\gamma = 180 - 38.36 - 59.04 = 82.6`

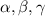
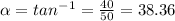
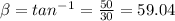
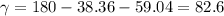
To Find tension in AC and magnitude R, use sine rule.

`(sin a)/(T_A_C) = (sin b)/(T_A_B) = (sin c)/(R)`

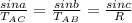
Substitute values:

`(sin 38.36)/(T_A_C) = (sin 59.04)/(8.7) = (82.6)/(R)`

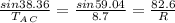
Solve for T_A_C:

`T_A_C = 8.7 * (sin 38.36)/(sin 59.04) =`

`T_A_C = 8.7 * 0.724 = 6.296 kN`

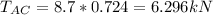
Solve for R.

`R = 8.7 * (sin 82.6)/(sin 59.04) =`

`R = 8.7 * 1.156`

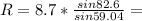
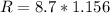
R = 10.06 kN

Tension AC = 6.296kN

Magnitude,R = 10.06 kN