Question

A flexible cable always hangs in the shape of a catenary curve y = c + a cosh(x/a), where cand a are constants, a > 0. Suppose a telephone line hangs between two poles 18 meters apart, in the shape of the catenary y = 30 cosh(x/15) - 4, where x and y are measured in meters. a. (3 pts.) Find the slope of this curve where it meets the right pole. (Round to 3 decimal places.] b. (3 pts.) Find the angle between the line and the right pole. [Give your answer in degrees, rounded to the nearest hundredth.) Expert Answer

Answer 1

The slope of this curve where it meets the right pole is 1.130

The angle between the line and the right pole is 41.51 °

Explanation:

Given that ;

`y = 30 \ cos h ((x)/(15) - 4)`

`(dy)/(dx)= (30)/(15) sinh((x)/(15))`

`(dy)/(dx)=2 \ sinh((x)/(15))`

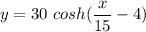
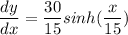
x = 9 m;( i.e half of the distance of the two poles at 18 meters apart.

`(dy)/(dx)=2 \ sinh((9)/(15))`

= 1.130

The slope of this curve where it meets the right pole is 1.130

The angle between the line an the right rope can be determined by using the tangent of the slope .

tan ∝ = 1.130

∝ = tan⁻¹ (1.130)

∝ = 48.49°

The angle is θ; so

θ = 90 - ∝

θ = 90 - 48.49°

θ = 41.51 °

Thus; the angle between the line and the right pole is 41.51 °