Question

Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval.

x4 + x ? 7 = 0, (1, 2)
f(x) = x4 + x ? 7
is (FILL IN)
a) defined
b) continuous
c) negative
d) positive on the closed interval [1, 2],
f(1) = ?? FILL IN , and f(2) = ?? FILL IN
Since ?5 < FILL IN a)? b)? c)? d)0 < 11, there is a number c in (1, 2) such that
f(c) = FILL IN a)? b)? c)0 d)11 e)-5
by the Intermediate Value Theorem. Thus, there is a FILL IN a) limit b)root c) discontinuity of the equation
x4 + x ? 7 = 0
in the interval (1, 2).

Answer 1

The correct option is d

`f(1) = -5`

`f(2) = 11`

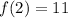
The correct option is d

The correct option is c

the correct option is b

Explanation:

The given equation is

`f(x) = x^4 + x -7 =0`

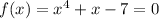
The give interval is
`(1,2)`

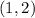
Now differentiating the equation

`f'(x) = 4x^3 +7 > 0`

Therefore the equation is positive at the given interval

Now at x= 1

`f(1) = (1)^4 + 1 -7 =-5`

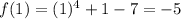
Now at x= 2

`f(2) = (2)^4 + 2 -7 =11`

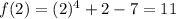
Now at the interval (1,2)

`f(1) < 0 < f(2)`

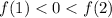
i.e

`-5 < 0 < 11`

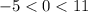
this tell us that there is a value z within 1,2 and

f(z) = 0

Which implies that there is a root within (1,2) according to the intermediate value theorem