Question

A bag contains 7 red and 10 white balls. In how many ways 4 balls are selected if there are more than 2 red balls? (Please solve it using counting rule; combination rule.)

Answer 1

385 ways

Explanation:

Given;

7 red balls

10 white balls

In how many ways can 4 balls be selected if there are more than 2 red balls.

Selecting 4 balls which must contain more than 2 red balls, will be 3 red balls and 1 white ball to make it 4 in total, or all the 4 balls selected will red balls.

= 3 red balls and 1 white ball OR 4 red balls

= 7C₃ x 10C₁ + 7C₄

`= (7!)/(4!3!) *(10!)/(9!1!) \ \ + \ (7!)/(3!4!) \\\\= (35*10) \ + \ 35\\\\= 350 \ + 35\\\\= 385 \ ways`

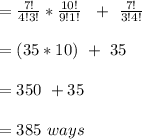
Therefore, there are 385 ways of selecting 4 balls, if there are more than 2 red balls.