Question

A ball travels on a parabolic path in which the height (in feet) is given by the expression $-25t^2+75t+24$, where $t$ is the time after launch. At what time is the height of the ball at its maximum?

Answer 1

The height of the ball is at it's maximum 1.5 units of time after launch.

Explanation:

Suppose we have a quadratic function in the following format:

`h(t) = at^(2) + bt + c`

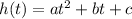
If t is negative, the maximu value of h(t) will happen at the point

`t_(MAX) = -(b)/(2a)`

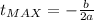
In this question:

`h(t) = -25t^(2) + 75t + 24`

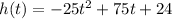
So

`a = -25, b = 75, c = 24`

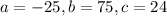
Then

`t_(MAX) = -(b)/(2a) = -(75)/(2*(-25)) = 1.5`

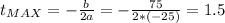
The height of the ball is at it's maximum 1.5 units of time after launch.