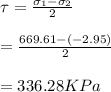Question

A cantilever beam with a width b=100 mm and depth h=150 mm has a length L=2 m and is subjected to a point load P =500 N at B. Calculate the state of plane stress at point C located 50 mm below the top of the beam and 0.5 m to the right of point A. Also find the principal stresses and the maximum shear stress at C. Neglect the weight of the beam.

Answer 1

Step-by-step explanation:

Given that:

width b=100mm

depth h=150 mm

length L=2 m =200mm

point load P =500 N

Calculate moment of inertia

`I=(bh^3)/(12) \\\\=(100 * 150^3)/(12) \\\\=28125000\ m m^4`

Point C is subjected to bending moment

Calculate the bending moment of point C

M = P x 1.5

= 500 x 1.5

= 750 N.m

M = 750 × 10³ N.mm

Calculate bending stress at point C

`\sigma=(M.y)/(I) \\\\=((750*10^3)(25))/(28125000) \\\\=0.0667 \ MPa\\\\ \sigma =666.67\ kPa`

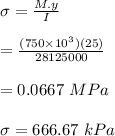
Calculate the first moment of area below point C

`Q=A \bar y\\\\=(50 * 100)(25 +(50)/(2) )\\\\Q=250000\ mm`

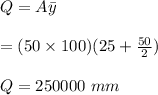
Now calculate shear stress at point C

`=(FQ)/(It)`

`=(500*250000)/(28125000*100) \\\\=0.0444\ MPa\\\\=44.4\ KPa`

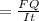
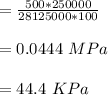
Calculate the principal stress at point C

`\sigma_(1,2)=(\sigma_x+\sigma_y)/(2) \pm\sqrt{((\sigma_x-\sigma_y)/(2) ) + (\tau)^2} \\\\=(666.67+0)/(2) \pm\sqrt{((666.67-0)/(2) )^2 \pm(44.44)^2} \ [ \sigma_y=0]\\\\=333.33\pm336.28\\\\ \sigma_1=333.33+336.28\\=669.61KPa\\\\\sigma_2=333.33-336.28\\=-2.95KPa`

Calculate the maximum shear stress at piont C

`\tau=(\sigma_1-\sigma_2)/(2)\\\\=(669.61-(-2.95))/(2) \\\\=336.28KPa`