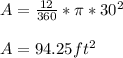Question

A carnival ride is in the shape of a wheel with the radius of 30 feet. The wheel has 30 cars attached to the center of the wheel. What is the central angle, arc length, and area of sector between any two cars? Round answers to the nearest hundredth if applicable. You must show all work and calculations to receive full credit.

Answer 1

α = 12°

L = 6.28 ft

`A = 94.25 ft^2`

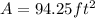
Explanation:

The wheel contains 30 cars attached to it.

The wheel is in the shape of a circle and a circle has 360°.

Therefore, the angle between any two cars will be:

360 / 30 = 12°

The length of the arc between two cars is given as:

`L = (\alpha )/(360) * 2\pi R`

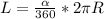
where α = central angle of sector

R = radius of circle

Given that the radius of the wheel is 30 feet, the length of the arc is:

`L = (12)/(360) * 2 * \pi * 30\\\\L = 6.28 ft`

The area of a sector is given by:

`A = (\alpha )/(360) * \pi R^2`

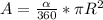
Therefore, the area of the sector between any two cars is:

`A = (12)/(360) * \pi * 30^2\\\\A = 94.25 ft^2`