Complete Question
The complete question is shown on the first uploaded image
Answer:
Part A
activation barrier for the reaction
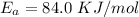
Part B
The frequency plot is

Step-by-step explanation:
From the question we are told that
at
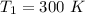
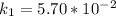
and at
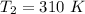
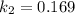
The Arrhenius plot is mathematically represented as
![ln [(k_2)/(k_1) ] = (E_a)/(R) [(1)/(T_1) - (1)/(T_2) ]](https://img.qammunity.org/2021/formulas/chemistry/college/utwsaampbj6ke4xqnmxntglbrjntrve475.png)
Where
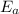 is the activation barrier for the reaction
is the activation barrier for the reaction
R is the gas constant with a value of
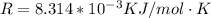
Substituting values
![ln [\frac{0.169}{6*10^-2{}} ] = (E_a)/(8.314*10^(-3)) [(1)/(300) - (1)/(310) ]](https://img.qammunity.org/2021/formulas/chemistry/college/xu3vkmr2h6e846auh6xow5wl0afajt44jj.png)
=>
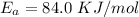
The Arrhenius plot can also be mathematically represented as
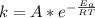
Here we can use any value of k from the data table with there corresponding temperature let take
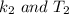
So substituting values
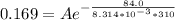
=>
