Answer:
Mega Gym charges a $384 registration fee and $2 each time the gym is used. Super Gym charges a fee of $6 every time the gym is used. What number of times, x, will Super Gym need to be used to exceed the cost of Mega Gym?
Explanation:
Given: the inequality is

To find: the correct option
Solution:
Let x denotes number of times gym is used.
As Mega Gym charges a $384 registration fee and $2 each time the gym is used,
Total amount charged by Mega Gym =
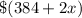
As Super Gym charges a fee of $6 every time the gym is used,
Total amount charged by Super Gym =
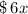
In order to find number of times, x Super Gym is used such that cost of Super Gym exceeds the cost of Mega Gym,
Solve the inequality:
cost of Super Gym > cost of Mega Gym

So, the correct option is '' Mega Gym charges a $384 registration fee and $2 each time the gym is used. Super Gym charges a fee of $6 every time the gym is used. What number of times, x, will Super Gym need to be used to exceed the cost of Mega Gym? ''