Answer:
10,080 different ways that the letters of "misspell" can be arranged.
Explanation:
Number of arrangents of the letters of a word:
A word has n letters.
The are m repeating letters, each of them repeating
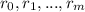 times
times
So the number of distincts ways the letters can be arranged is:
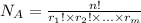
In this question:
Misspell has 8 letters, with s and l repeating twice.
So
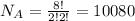
10,080 different ways that the letters of "misspell" can be arranged.