Question

Is the function given by ​f(x)equalsleft brace Start 2 By 2 Matrix 1st Row 1st Column one fourth x plus 1 comma 2nd Column for x less than or equals 4 comma 2nd Row 1st Column 4 x minus 11 comma 2nd Column for x greater than 4 comma EndMatrix continuous at xequals4​? Why or why​ not? Choose the correct answer below. A. The given function is continuous at xequals4 because ModifyingBelow lim With x right arrow 4 f (x )does not exist. B. The given function is not continuous at xequals4 because ​f(4​) does not exist. C. The given function is continuous at xequals4 because the limit is 2. D. The given function is not continuous at xequals4 because ModifyingBelow lim With x right arrow 4 f (x )does not exist.

Answer 1

C. The given function is continuous at x=4 because the limit is 2.

Explanation:

Given the function:

`f(x)=\left\{\begin{array}{ccc}(1)/(4)x+1 &x\leq 4\\4x-11&x>4\end{array}\right`

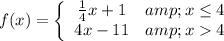
We are to determine if the function is continuous at x=4.

For a function to be continuous at some value c in its domain:

• f(c) must be defined.

• 
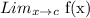  `Lim_(x \to c)$ f(x)` must exist.

• 
  `f(c)=Lim_(x \to c)$ f(x)`

Now: at x=4

• 
  `f(4)=(1)/(4)*4+1=2`

• 
  `Lim_(x \to 4)f(x)=2`

Since the two values are the same, we say that f(x) is continuous at x=4.

The correct option is C.