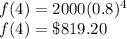Question

A powerful computer is purchased for $2000, but loses 20% of its value each year. How much will it be worth 4 years from now?

a. Growth or Decay?


b. What is your multiplier?


c. Is $2000 your zero term or first term? term


d. Write the equation. (do not use spaces in your response; example: f(x)=10.2(1.22)^x )


e. Solve

Answer 1

(A)Decay

(b)0.8

(c)First Term

(d)
`f(t)=2000(0.8)^t`

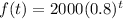
(e)$819.20

Explanation:

The exponential function for modelling growth or decay is given as:

`A(t)=A_o(1\pm r)^t`,

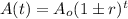Where:

Plus indicates growth and minus indicates decay.

`A_o$ is the Initial Value\\r is the growth/decay rate\\t is the time period`

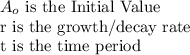
For a powerful computer that was purchased for $2000, but loses 20% of its value each year.

(a)Since it loses value, it is a decay.

(b)Multiplier

Its value decays by 20%.

Therefore, our multiplier(1-r) =(1-20&)=1-0.2

Multiplier =0.8

(c)$2000 is our First term (or Initial Value
`A_o`)

(d)The function for this problem is therefore:

`f(t)=f_o(1- r)^t\\f(t)=2000(1- 0.2)^t\\\\f(t)=2000(0.8)^t`

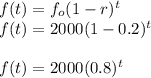
(e)Since we require the worth of the computer after 4 years,

t=4 years

`f(4)=2000(0.8)^4\\f(4)=\$819.20`