Question

Ronald throws a football at an intial velocity of 20 ft per sec. He releases the ball at a height of 5 feet.

1) What is the height of the football at time 2.25 seconds?
2) When does this football reach the highest point of its flight?
3) When does this football hit the ground?

Answer 1

1) the football already reached the ground

2) t = 0.625 seconds

3) t = 1.46 seconds

Explanation:

Data

• initial velocity, Vi = 20 ft/s

• initial height, Hi = 5 feet.

• gravitational acceleration, g = 32 ft/s²

1) time, t = 2.25 s

To relate these variables we need to use the next equation:

H = Hi + Vi*t - 1/2*g*t²

H = 5 + 20*2.25 - 1/2*32*2.25²

H = -31 ft

that is, 31 ft under the line of reference. This means that the football already reached the ground

2) At the highest point the final velocity (Vf) is zero.

To relate these variables we need to use the next equation:

Vf = Vi - g*t = 0

Vi = g*t

t = Vi/g

t = 20/32

t = 0.625 s

3) When the football hits the ground, ΔH = -5 ft. Then:

ΔH = Vi*t - 1/2*g*t²

-5 = 20*t - 1/2*32*t²

0 = -16t² + 20t + 5

Using quadratic formula:

`t = (-b \pm √(b^2 - 4(a)(c)))/(2(a))`

`t = (-20 \pm √(20^2 - 4(-16)(5)))/(2(-16))`

`t = (-20 \pm 26.83)/(-32)`

`t_1 = (-20 + 26.83)/(-32)`

`t_1 = -0.21`

`t_2 = (-20 - 26.83)/(-32)`

`t_2 =1.46`

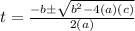
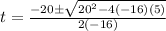
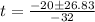
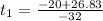
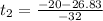
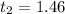
The first result is discarded because it doesn't have physical sense. So, the football hit the ground after 1.46 seconds